Question

The game of blackjack played with one​ deck, a player is initially dealt 2 different cards from the 52 different cards in the deck. A winning​ "blackjack" hand is won by getting 1 of the 4 aces and 1 of 16 other cards worth 10 points. The two cards can be in any order. Find the probability of being dealt a blackjack hand. What approximate percentage of hands are winning blackjack​ hands?

Answer 1

After completing this question, I got the calculation that the probability of being dealt a blackjack hand is 32/663. The percentage is 4.83%, or as a decimal ~0.0483

Answer 2

a) The probability of being dealt a blackjack hand

`= (64)/(1326)`

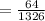
b) Approximate percentage of hands winning blackjack​ hands

`4.827%`

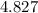
Explanation:

It is given that -

Winning Black Jack means - getting 1 of the 4 aces and 1 of 16 other cards worth 10 points

Thus, in order to win a "black jack" , one is required to pull 1 ace and 1 of 16 other cards

Number of ways in which an ace card can be drawn from a set of 4 ace card is
`C^4_1`

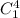
Number of ways in which one card can be drawn from a set of other 16 card is
`C^16_1`

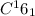
Number of ways in which two cards are drawn from a set of 52 cards is
`C^52_2`

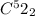
probability of being dealt a blackjack hand

`= (C^4_1* C^16_1)/(C^52_2) \\= (4*16)/((51*52)/(2) )\\ = (64)/(1326) \\`

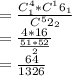
Approximate percentage of hands winning blackjack​ hands

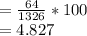`= (64)/(1326) * 100\\= 4.827`%