Question

A 1024 Hz tuning fork is used to obtain a series of resonance levels in a gas column of variable length, with one end closed and the other open. The length of the column changes by 20 cm from resonance to resonance. From this data, the speed of sound in this gas is:

Answer 1

The speed of sound in this gas is 409.6 m/s.

Step-by-step explanation:

The length of the column changes from 20 cm from resonance to resonance. Thus,

`L=\frac {(2n+1)\lambda}{4}`

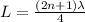
The length change from one resonance to resonance. so, there is 1 loop change. So,

ΔL = 1 loop = λ/2

ΔL = 20 cm (given)

Also, 1 cm = 0.01 m

So,

ΔL = 0.2 cm (given)

The wavelength is:

λ = ΔL×2

λ = 2x0.2 = 0.4 m

Given:

Frequency (ν) = 1024 Hz

Velocity of the sound in the gas = ν×λ = 1024×0.4 m/s = 409.6 m/s