Answer:
The average separation is 0.002041 AU
Step-by-step explanation:
Given data:
Mass of the neutron star, M₁ = 2.5
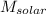
Mass of the White dwarf, M₂ = 0.3
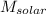
Orbiting period (P)= 28 minutes
1 year = 365 × 24 × 60 minutes = 525600 minutes
or
1 minute = 1/525600 years
thus, 28 minutes = 28/525600 years = 5.327 × 10⁻⁵ years
now from the Kepler's third law we have,
MP² = a³
where, P is the period
M is the mass = M₁ + M₂
a is the size of the orbit
thus, by substituting the values in the equation we get
(2.5
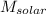 +0.3
+0.3
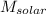 )(5.327 × 10⁻⁵ years)² = a³
)(5.327 × 10⁻⁵ years)² = a³
Also,
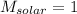 when planets orbiting sun
when planets orbiting sun
thus,
2.8 ×(5.327 × 10⁻⁵ years)² = a³
or
a³ = 7.94 × 10⁻⁹
or
a = 1.99 × 10⁻³ AU
thus, the average separation is 0.001995 AU
Now
1 AU = 1.5 × 10⁸ km
thus,
0.001995 AU = 299281.61 km = 2.99 × 10⁵ km
in terms of sun's radius = (2.99 × 10⁵ km)/(7 ×10⁵) = 0.427
Thus, the this orbit system will fit inside the sun