Answer:
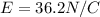
and its direction must be horizontal and towards the wall
Step-by-step explanation:
As we know that string is attached to the vertical wall
Now the string is connected to the ball with mass 13 g
so ball will have two forces on it
1) Gravitational force due to its own mass
2) electrostatic force due to electric field
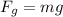
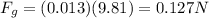
now electrostatic force will be in horizontal direction given as
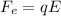
Now given that string makes 17.4 degree angle with the vertical wall
so we can say
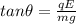
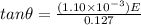
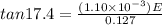
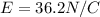
and its direction must be horizontal and towards the wall