Question

A small 13.0-g plastic ball is tied to a very light 27.2-cm string that is attached to the vertical wall of a room (Fig. P21.65). A uniform horizontal electric field exists in this room. When the ball has been given an excess charge of -1.10 mC, you observe that it remains suspended, with the string making an angle of 17.4° with the wall. Find the magnitude and direction of the electric field in the room.

Answer 1

`E = 36.2 N/C`

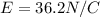
and its direction must be horizontal and towards the wall

Step-by-step explanation:

As we know that string is attached to the vertical wall

Now the string is connected to the ball with mass 13 g

so ball will have two forces on it

1) Gravitational force due to its own mass

2) electrostatic force due to electric field

`F_g = mg`

`F_g = (0.013)(9.81) = 0.127 N`

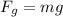
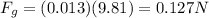
now electrostatic force will be in horizontal direction given as

`F_e = qE`

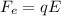
Now given that string makes 17.4 degree angle with the vertical wall

so we can say

`tan\theta = (qE)/(mg)`

`tan\theta = ((1.10 * 10^(-3))E)/(0.127)`

`tan17.4 = ((1.10 * 10^(-3))E)/(0.127)`

`E = 36.2 N/C`

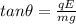
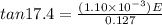
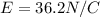
and its direction must be horizontal and towards the wall