Question

Given the Arithmetic sequence A1,A2,A3,A4 53, 62, 71, 80 What is the value of A38?

Answer 1

`A_(38)=386`

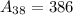
Explanation:

We have been given an arithmetic sequence gas
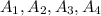`A_1,A_2,A_3,A_4` as :53,62,71,80. We are asked to find
`A _(38)`.

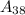We know that an arithmetic sequence is in format
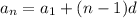`a_n=a_1+(n-1)d`, where,

`a_n` = nth term,

`a_1` = 1st term of sequence,

n = Number of terms,

d = Common difference.

We have been given that 1st term of our given sequence is 53.

Now, we will find d by subtracting 71 from 80 as:

`d=80-71=9`

`A_(38)=53+(38-1)9`

`A_(38)=53+(37)9`

`A_(38)=53+333`

`A_(38)=386`

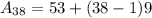
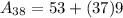
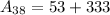
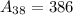
Therefore,
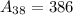`A_(38)=386`.

Answer 2

`A_(38) = 350`

Explanation:

The 5th term of the arithmetic sequence is 53. We can write the equation:

`a + 4d = 53...(1)`

The 6th term of the arithmetic sequence is 62. We can write the equation:

`a + 5d = 62...(2)`

Subtract the first equation from the second one to get:

`5d - 4d = 62 - 53`

`d = 9`

The first term is

`a + 4(9) = 53`

`a + 36 = 53`

`a = 53 - 36`

`a = 17`

The 38th term of the sequence is given by:

`A_(38) = a + 37d`

`A_(38) = 17+ 37(9)`

`A_(38) = 350`