Question

A simple random sample of size nequals40 is drawn from a population. The sample mean is found to be 103.9​, and the sample standard deviation is found to be 21.9. Is the population mean greater than 100 at the alphaequals0.05 level of​ significance?

Answer 1

There is enough evidence to support the claim that the population mean is greater than 100

Explanation:

Step 1: We state the hypothesis and identify the claim

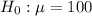`H_0:\mu=100` and
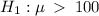`H_1:\mu \:>\:100` (claim)

Step 2: Calculate the test value.

`t=(\bar X-\mu)/((s)/(√(n) ) )`

`\implies t=(103.9-100)/((21.9)/(√(40) ) )=1.1263`

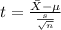
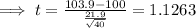
Step 3: Find the P-value. The p-value obtained from a calculator is using d.f=39 and test-value 1.126 is 0.134

Step 4: We fail to reject the null hypothesis since P-value is greater that the alpha level. (0.134>0.05).

Step 5: There is enough evidence to support the claim that the population mean is greater than 100.

Alternatively: We could also calculate the critical value to obtain +1.685 for
`\alpha=0.05` and d.f=39 and compare to the test-value:

The critical value (1.685>1.126) falls in the non-rejection region. See attachment.

NB: The t- distribution must be used because the population standard deviation is not known.