Question

The sum of the interior angles, s, in an n-sided polygon can be determined using the formula s=180(n−2), where n is the number of sides.

Using this formula, how many sides does a polygon have if the sum of the interior angles is 1,260°? Round to the nearest whole number.

Answer 1

Answer: d

Explanation:

Answer 2

The polygon has 9 sides

Explanation:

We need to equate the given expression to the given value and solve for n.

The sum of the interior angles, s, in an n-sided polygon is given by the expression:

`s = 180(n - 2)`

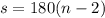
We want to use this formula, to calculate how many sides has a polygon if the sum of the interior angles is 1,260°.

We solve the following equation for n.

`180(n - 2) = 1260`

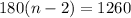
Divide through by 180 to get:

`(180(n - 2))/(180) = (1260)/(180)`

`n - 2 = 7`

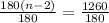
Add 2 to both sides to get:

`n = 7 + 2`

`\therefore \: n = 9`

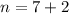
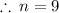
Hence the polygon has 9 sides