Question

Coherent light of frequency 6.37×1014 Hz passes through two thin slits and falls on a screen 88.0 cm away. You observe that the third bright fringe occurs at ± 3.10 cm on either side of the central bright fringe. How far apart are the two slits?

Answer 1

The distance between the two slits is 40.11 μm.

Step-by-step explanation:

Given that,

Frequency
`f= 6.37*10^(14)\ Hz`

Distance of the screen l = 88.0 cm

Position of the third order y =3.10 cm

We need to calculate the wavelength

Using formula of wavelength

`\lambda=(c)/(f)`

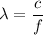
where, c = speed of light

f = frequency

Put the value into the formula

`\lambda=(3*10^(8))/(6.37*10^(14))`

`\lambda=471\ nm`

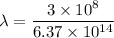
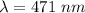
We need to calculate the distance between the two slits

`m* \lambda=d\sin\theta`

`d =(m*\lambda)/(\sin\theta)`

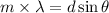
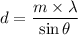
Where, m = number of fringe

d = distance between the two slits

Here,
`\sin\theta =(y)/(l)`

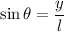
Put the value into the formula

`d=(3*471*10^(-9)*88.0*10^(-2))/(3.10*10^(-2))`

`d=40.11*10^(-6)\ m`

`d = 40.11\ \mu m`

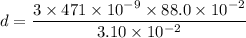
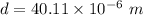
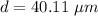
Hence, The distance between the two slits is 40.11 μm.