Question

A committee of 4 people to be formed from a pool of 15 students ( 7 from UCF and 8 from UF). In how many ways can that be done knowing that every committee must have at least one UCF student?

Answer 1

Answer: 2863

Explanation:

Given : The number of UCF students = 7

The number of UF students = 8

If a committee of 4 people to be formed , then the number of ways to form the committee such that every committee must have at least one UCF student is given by :-

`^7C_4\cdot ^8C_0+^7C_3\cdot ^8C_1+^7C_2\cdot ^8C_2+^7C_1\cdot ^8C_3\\\\=(7!)/(4!(7-4)!)*1+(7!)/(3!(7-3)!)* (8!)/(1!(8-1)!)+(7!)/(2!(7-2)!)*(8!)/(2!(8-2)!)+(7!)/(1!(7-1)!)*(8!)/(3!(7-3)!)\\\\=35+280+588+1960=2863`

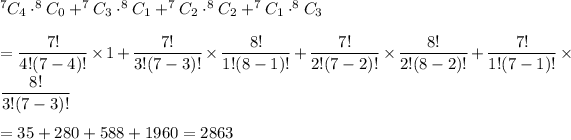
Hence, there are 2863 ways to form the committee which must have at least one UCF student .