Answer:
The time taken by the jet is 6.44 seconds.
Explanation:
It is given that,
Acceleration of the jet,

Initial velocity of the jet, u = 119 m/s
Final velocity of the jet, v = 233 m/s
Acceleration of an object is given by :
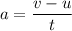
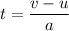
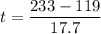
t = 6.44 seconds
So, the time taken by the jet is 6.44 seconds. Hence, this is the required solution.