Answer: 0.30
Explanation:
Binomial distribution formula :-
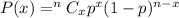 , where P(x) is the probability of getting success in x trials , n is the total number of trials and p is the probability of getting success in each trial.
, where P(x) is the probability of getting success in x trials , n is the total number of trials and p is the probability of getting success in each trial.
Given : The probability that a shipment are known to be defective= 0.07
If a sample of 5 items is randomly selected from this shipment,then the probability that at least one defective item will be observed in this sample will be :-

Hence, the probability that at least one defective item will be observed in this sample =0.30