Answer:
 = 591.45 T/s
= 591.45 T/s
Step-by-step explanation:
i = induced current in the loop = 0.367 A
R = Resistance of the loop = 117 Ω
E = Induced voltage
Induced voltage is given as
E = i R
E = (0.367) (117)
E = 42.939 volts
 = rate of change of magnetic field
= rate of change of magnetic field
A = area of loop = 7.26 x 10⁻² m²
Induced emf is given as

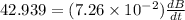
 = 591.45 T/s
= 591.45 T/s