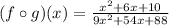Answer:
The domain is all real numbers where
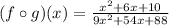
Explanation:
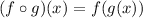
So g(x) must exist before plugging it into f(x).
Let's find where g(x) doesn't exist.
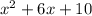 is a quadratic expression.
is a quadratic expression.
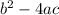 is the discriminant and will tell us if
is the discriminant and will tell us if
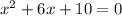 will have any solutions. I'm trying to solve this equation because I want to figure out what to exclude from the domain. Depending on what
will have any solutions. I'm trying to solve this equation because I want to figure out what to exclude from the domain. Depending on what
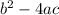 we may not have to go full quadratic formula on this problem.
we may not have to go full quadratic formula on this problem.
 .
.
Since the discriminant is negative, then there are no real numbers that will make the denominator 0 here. So we have no real domain restrictions on g.
Let's go ahead and plug g into f.
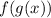
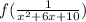
I replaced g(x) with (1/(x^2+6x+10)).
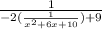
I replaced old input,x, in f with new input (1/(x^2+6x+10)).
Let's do some simplification now.
We do not like the mini-fraction inside the bigger fraction so we are going to multiply by any denominators contained within the mini-fractions.
I'm multiplying top and bottom by (x^2+6x+10).
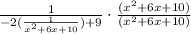
Using distributive property:
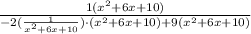
We are going to distribute a little more:
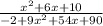
Combine like terms on the bottom there (-2 and 90):

Now we can see if we have any domain restrictions here:

So again the bottom will never be zero because
 doesn't have any real solutions. We know this because the discriminant is negative.
doesn't have any real solutions. We know this because the discriminant is negative.
The domain is all real numbers where