Question

Which of the following polynomials represents a difference of squares? x^2-1,x^2-8,4x^2+16,9x^2-18

Answer 1

`x^(2) -1`

Explanation:

we know that

Every difference of squares problem can be factored as follows:

`a^(2)-b^(2)=(a+b)(a-b)`

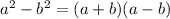
If the polynomial represent a difference of squares every number must be a perfect square (Remember that a number is a perfect square if its square root is an integer.)

Verify each case

case 1) we have

`x^(2) -1`

In this case both numbers are perfect square

so

`x^(2) -1=(x+1)(x-1)`

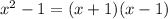
therefore

The polynomial represent a difference of squares

case 2) we have

`x^(2) -8`

In this case 8 is not a perfect square

therefore

The polynomial not represent a difference of squares

case 3) we have

`4x^(2) +16`

`4x^(2)+16=4(x^(2)+4)`

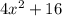
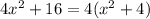
In this case both numbers are perfect square

but is a sum of squares

therefore

The polynomial not represent a difference of squares

case 4) we have

`9x^(2)-18`

`9x^(2)-18=9(x^(2)-2)`

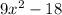
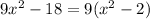
In this case 2 is not a perfect square

therefore

The polynomial not represent a difference of squares