Question

g Water use in the summer is normally distributed with a mean of 310.4 million gallons per day and a standard deviation of 40 million gallons per day. City reservoirs have a combined storage capacity of 350 million gallons. The probability that a day requires more water than is stored in city reservoirs is P(X > 350)= 1 - P (Z < b). What is the value of b? Please report your answer in 3 decimal places.

Answer 1

Answer: The value of b = 0.99

The probability that a day requires more water than is stored in city reservoirs is 0.161.

Explanation:

Given : Water use in the summer is normally distributed with

`\mu=310.4\text{ million gallons per day}`

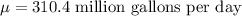
Standard deviation :
`\sigma=40 \text{ million gallons per day}`

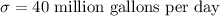
Let x be the combined storage capacity requires by the reservoir on a random day.

Z-score :
`(x-\mu)/(\sigma)`

`z=(350-310.4)/(40)=0.99`

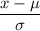
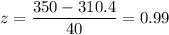
The probability that a day requires more water than is stored in city reservoirs is :

`P(x>350)=P(z>0.99)=1-P(z<0.99)\\\\=1-0.8389129=0.1610871\approx0.161`

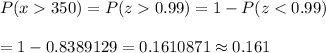
Hence, the probability that a day requires more water than is stored in city reservoirs is 0.161