Final Answer:
The volume of the prism is
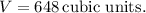
Step-by-step explanation:
The formula for the volume (V) of a rectangular prism is given by
 where (l) is the length, (w) is the width, and (h) is the height. In this case, the provided dimensions are length (l = 18), width (w = 9), and height (h = 4). Substituting these values into the formula:
where (l) is the length, (w) is the width, and (h) is the height. In this case, the provided dimensions are length (l = 18), width (w = 9), and height (h = 4). Substituting these values into the formula:
![\[ V = 18 * 9 * 4 = 648 \, \text{cubic units}. \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nnq7zhdsfvwbx7mml758bakfv8f977pns0.png) Therefore, the volume of the prism is
Therefore, the volume of the prism is
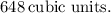
Understanding the concept of volume in three-dimensional geometry is vital. The formula
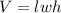 reflects the relationship between the length, width, and height of a rectangular prism. Multiplying these dimensions provides the total space enclosed by the prism in cubic units. In this instance, with a length of 18 units, a width of 9 units, and a height of 4 units, the volume calculation yields
reflects the relationship between the length, width, and height of a rectangular prism. Multiplying these dimensions provides the total space enclosed by the prism in cubic units. In this instance, with a length of 18 units, a width of 9 units, and a height of 4 units, the volume calculation yields
 representing the spatial capacity of the given prism.
representing the spatial capacity of the given prism.
Calculating the volume of prisms is a fundamental skill in geometry and has practical applications in various fields, including architecture and engineering. This calculation allows us to quantify the amount of space a three-dimensional object occupies, providing essential information for design and analysis. In this case, the resulting volume,
 represents the capacity of the rectangular prism specified by the given dimensions.
represents the capacity of the rectangular prism specified by the given dimensions.