Question

A researcher wishes to estimate the proportion of adults who have​ high-speed Internet access. What size sample should be obtained if she wishes the estimate to be within 0.05 with 95​% confidence if ​(a) she uses a previous estimate of 0.32​? ​(b) she does not use any prior​ estimates?

Answer 1

Answer: a) 8359 b) 384

Explanation:

Given : Significance level :
`\alpha=1-0.95=0.05`

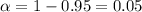
Critical value :
`z_(\alpha/2)}=\pm1.96`

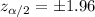
Margin of error :
`E=0.01`

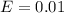
a) If previous estimate of proportion :
`p=0.32`

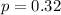
Formula to calculate the sample size needed for interval estimate of population proportion :-

`n=p(1-p)((z_(\alpha/2))/(E))^2`

`\Rightarrow\ n=0.32(1-0.32)((1.96)/(0.01))^2=8359.3216\approx 8359`

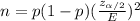
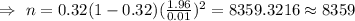
Hence, the required sample size would be 8359 .

b) If she does not use any prior estimate , then the formula to calculate sample size will be :-

`n=0.25*((z_(\alpha/2))/(E))^2\\\\\Rightarrow\ n=0.25*((1.96)/(0.05))^2=384.16\approx384`

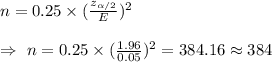
Hence, the required sample size would be 384 .