Answer: a) 8359 b) 384
Explanation:
Given : Significance level :

Critical value :
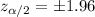
Margin of error :

a) If previous estimate of proportion :
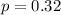
Formula to calculate the sample size needed for interval estimate of population proportion :-
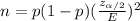
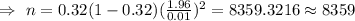
Hence, the required sample size would be 8359 .
b) If she does not use any prior estimate , then the formula to calculate sample size will be :-

Hence, the required sample size would be 384 .