Question

Prove that the median to the hypotenuse of a right triangle is half the hypotenuse.

Plan: Since midpoints will be involved, use multiples of __ to name the coordinates for M and N.

Answer 1

The correct option is D.

Explanation:

Given: ΔMNO is a right angled triangle with right angle ∠MON, P is midpoint of MN.

To prove:
`OP=(1)/(2)MN`

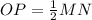
Since midpoints will be involved, use multiples of _2_ to name the coordinates for M and N.

Let the coordinates for M and N are (0,2m) and (2n,0) receptively.

Midpoint formula:

`Midpoint=((x_1+x_2)/(2),(y_1+y_2)/(2))`

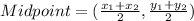
The coordinates of P are

`Midpoint=((2n+0)/(2),(2m+0)/(2))`

`Midpoint=(n,m)`

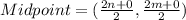
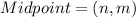
The coordinates of P are (n,m).

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Using distance formula, the distance between O(0,0) and P(n,m) is

`OP=√((n-0)^2+(m-0)^2)=√(n^2+m^2)`

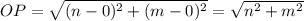
Using distance formula, the distance between M(0,2m) and N(2n,0) is

`MN=√((2n-0)^2+(0-2m)^2)`

`MN=√(4n^2+4m^2)`

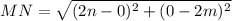
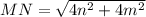
On further simplification we get

`MN=√(4(n^2+m^2))`

`MN=2√((n^2+m^2))`

`MN=2(OP)`

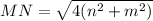
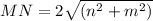
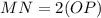
Divide both sides by 2.

`(1)/(2)MN=OP`

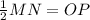
Interchange the sides.

`OP=(1)/(2)MN`

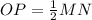
Hence proved.

Therefore, the correct option is D.

Answer 2

D. 2

Explanation:

Since midpoints will be involved, use multiples of 2 to name the coordinates for M and N.

Let

• M(0,2b)
• N(2a,0)

Then the midpoint P coordinates are

`P\left((2a+0)/(2),(0+2b)/(2)\right)\Rightarrow P(a,b)`

Use distance formula to find OP and MN:

`OP=√((a-0)^2+(b-0)^2)=√(a^2+b^2)\\ \\MN=√((2a-0)^2+(2b-0)^2)=√(4a^2+4b^2)=2√(a^2+b^2)`

So,

MN=2OP

or

OP=1/2 MN