Answer:
The correct option is D.
Explanation:
Given: ΔMNO is a right angled triangle with right angle ∠MON, P is midpoint of MN.
To prove:
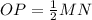
Since midpoints will be involved, use multiples of _2_ to name the coordinates for M and N.
Let the coordinates for M and N are (0,2m) and (2n,0) receptively.
Midpoint formula:
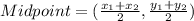
The coordinates of P are
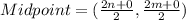
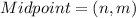
The coordinates of P are (n,m).
Distance formula:
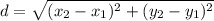
Using distance formula, the distance between O(0,0) and P(n,m) is
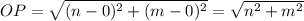
Using distance formula, the distance between M(0,2m) and N(2n,0) is
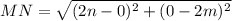
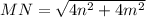
On further simplification we get
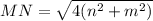
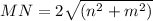
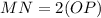
Divide both sides by 2.
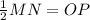
Interchange the sides.
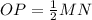
Hence proved.
Therefore, the correct option is D.