Answer:
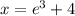 (exact)
(exact)
x = 24.0855 (rounded)
Explanation:
We need to remember 3 rules:
1. ln means log_e (ln is log base e)
2.
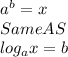
3.
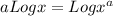
Now we can write the equation as:
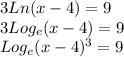
Now, we can convert it to exponential and solve:
![Log_e(x-4)^3=9\\(x-4)^3=e^9\\\sqrt[3]{(x-4)^3}=\sqrt[3]{e^9} \\ x-4=e^3\\x=e^3+4](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tljs44m6sj7oouv0cpl5gpltj9tr77ak4v.png)
This is the exact value of x, in 4 decimal places (by using calculator), it would be
x = 24.0855