Answer:
We have the following function:
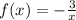
The graph of this function has been plotted below. So lets analyze each statement:
1. The function is always increasing.
False
As you can see x increases from -∞ to 0 and decreases from 0 to +∞
2. The function has a domain of all real numbers.
False
The function is undefined for
 since x is in the denominator.
since x is in the denominator.
3. The function has a range of {yl-
Statement is unclear but the range is the set of all real numbers except zero.
4. The function is a reflection of y = 3.
False
The function is a reflection in the x axis of the function

5. The function passes through the point (3,-27).
False
This is false since:
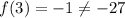
Note. As you can see those statements are false, so any of them is true, except item 3 that is unclear.