Answer:
Point (1 , 6) is on the circle
Explanation:
* Lets explain how to solve the problem
- The equation of the circle with center (h , k) and radius r is:
(x - h)² + (y - k)² = r²
- To prove that a point lies on the circle , substitute x , y in the
equation by the coordinates of this point if the left hand side of
the equation equals the right hand side that means the point
satisfies the equation then the point lies on the circle
* Lets use this fact to solve the problem
∵ The center of the circle is (1 , 1)
∴ h = 1 , k = 1
∵ The point (-3 , 4) lies on the circle
∴ The distance between the center of the circle (1 , 1) and the point
(-3 , 4) is the radius of the circle
- The rule of the distance between points(x1 , y1) and (x2 , y2) is
d = √[(x2 - x1)² + (y2 - y1)²]
∵ (1 , 1) is (x1 , y1) and (-3 , 4) is (x2 , y2)
∴ x1 = 1 , x2 = -3 and y1 = 1 , y2 = 4
- Lets calculate r using the rule of the distance above
∴
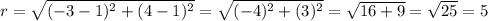
∴ The radius of the circle is 5 units
∵ The equation of the circle is (x - h)² + (y - k)² = r²
∵ h = 1 , k = 1 , r = 5
∴ (x - 1)² + (y - 1)² = 25
∴ The equation of the circle is (x - 1)² + (y - 1)² = 25
- Lets substitute x and y in the equation by the coordinates of
point (1 , 6)
∵ x = 1 and y = 6
∵ L.H.S ⇒ (1 - 1)² + (6 - 1)² = (0)² + (5)² = 0 + 25 = 25
∵ R.H.S ⇒ 25
∴ L.H.S = R.H.S
∴ Point (1 , 6) is on the circle