Question

There is a 60 percent chance of low demand and a 40 percent chance of high demand. The corresponding (inverse) demand functions for these two scenarios are P = 300,000 – 400Q and P = 500,000 – 275Q, respectively. Your cost function is C(Q) = 140,000 + 240,000Q. How many new homes should you build, and what profits can you expect?

Answer 1

New houses build =200

Profit =$13,860,000

Step-by-step explanation:

In this particular question there are 2 scenarios for demand function,

i.e. (a.) 60 percent chance of low demand,
`P_(60)  = 300,000-400Q`

(b.) 40 percent chance of high demand,
`P_(40)  = 500,000-275Q`

∴ Expected demand function = 60%×(300000-400Q) + 40%×(500000-275Q)

= 380,000-350Q

`P_(D)` =380000-350Q

Revenue = (380000 - 350Q)×Q = 380000Q - 350
`Q^(2)`

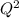
Here, the no. of new homes build will depend on maximizing profit

∵ Profit = Revenue - Cost

π = (380000 - 350Q)×Q - (140000+240000Q)

π = 380000Q - 350
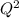`Q^(2)` - (140000+240000Q)

In order to maximize profit , we will

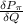`(\delta P_(\pi))/(\delta Q)` = 0

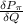`(\delta P_(\pi))/(\delta Q)` = 380000-350*2*Q-240000

∴ 380000-350×2×(Q-240000) =0

Q=200

So number of houses that they should build =200

π = 380000Q - 350
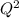`Q^(2)` - (140000+240000Q)

π = 380000-(350×
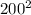`200^(2)`) - (140000+(240000*200))

π =$13,860,000

New houses to be build =200

Profit =$13,860,000