A curve passes through the point (0, 5) and has the property that the slope of the curve at every point P is twice the y-coordinate of P. What is the equation of the curve? (Use…

Question

asked Dec 11, 2020 36.4k views

1 Answer

Itun · Answer 1 · 2020-12-15T13:25:06+0000

Answer:

y=5e^(2x)

Explanation:

Let (x,y) represents a point P on the curve,

So, the slope of the curve at point P =
(dy)/(dx)

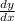
According to the question,

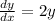
(dy)/(dx)=2y

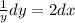
(1)/(y)dy=2dx

Integrating both sides,

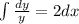
$\int (dy)/(y)=2dx$

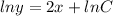
ln y=2x+ln C

ln y-ln C = 2x

ln((y)/(C))=2x

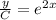
(y)/(C)=e^(2x)

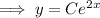
$\implies y=Ce^(2x)$

Since, the curve is passing through the point (0, 5),

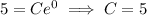
$5=Ce^(0)\implies C=5$

Hence, the required equation of the curve is,

y=5e^(2x)