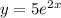Answer:
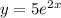
Explanation:
Let (x,y) represents a point P on the curve,
So, the slope of the curve at point P =
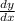
According to the question,
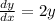
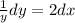
Integrating both sides,
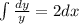
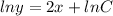
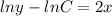
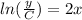
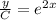
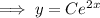
Since, the curve is passing through the point (0, 5),
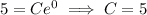
Hence, the required equation of the curve is,