Question

Please help prove these identities!

Answer 1

Hi! It will be a pleasure to help you to prove these identities, so let's get started:

PART a)

We have the following expression:

`tan(\theta)cot(\theta)-sin^(2)(\theta)=cos^2(\theta)`

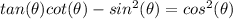
We know that:

`cot(\theta)=(1)/(cot(\theta))`

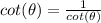
Therefore, by substituting in the original expression:

`tan(\theta)\left((1)/(tan(\theta))\right)-sin^(2)(\theta)=cos^2(\theta) \\ \\ \\ Simplifying: \\ \\ 1-sin^2(\theta)=cos^2(\theta)`

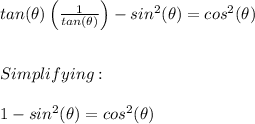
We know that the basic relationship between the sine and the cosine determined by the Pythagorean identity, so:

`sin^2(\theta)+cos^2(\theta)=1`

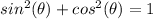
By subtracting
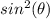`sin^2(\theta)` from both sides, we get:

`\boxed{cos^2(\theta)=1-sin^2(\theta)} \ Proved!`

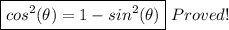
PART b)

We have the following expression:

`(cos(\alpha))/(cos(\alpha)-sin(\alpha))=(1)/(1-tan(\alpha))`

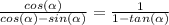
Here, let's multiply each side by
`cos(\alpha)-sin(\alpha)`:

`(cos(\alpha)-sin(\alpha))\left((cos(\alpha))/(cos(\alpha)-sin(\alpha))\right)=(cos(\alpha)-sin(\alpha))\left((1)/(1-tan(\alpha))\right) \\ \\ Then: \\ \\ cos(\alpha)=(cos(\alpha)-sin(\alpha))/(1-tan(\alpha))`

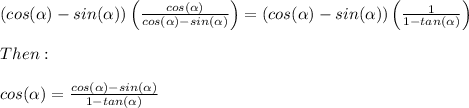
We also know that:

`tan(\alpha)=(sin(\alpha))/(cos(\alpha))`

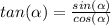
Then:

`cos(\alpha)=(cos(\alpha)-sin(\alpha))/(1-(sin(\alpha))/(cos(\alpha))) \\ \\ \\ Simplifying: \\ \\ cos(\alpha)=(cos(\alpha)-sin(\alpha))/((cos(\alpha)-sin(\alpha))/(cos(\alpha))) \\ \\ Or: \\ \\ cos(\alpha)=((cos(\alpha)-sin(\alpha))/(1))/((cos(\alpha)-sin(\alpha))/(cos(\alpha))) \\ \\ Then: \\ \\ cos(\alpha)=cos(\alpha).(cos(\alpha)-sin(\alpha))/(cos(\alpha)-sin(\alpha)) \\ \\ \boxed{cos(\alpha)=cos(\alpha)} \ Proved!`

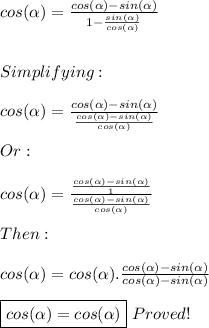
PART c)

We have the following expression:

`(cos(x+y))/(cosxsiny)=coty-tanx`

From Angle Sum Property, we know that:

`cos(x+y)=cos(x)cos(y)-sin(x)sin(y)`

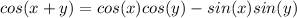
Substituting this in our original expression, we have:

`(cos(x)cos(y)-sin(x)sin(y))/(cosxsiny)=coty-tanx`

But we can also write this as follows:

`\\ (cosxcosy)/(cosxsiny)-(sinxsiny)/(cosxsiny)=coty-tanx \\ \\ Simplifying: \\ \\ (cosy)/(siny)-(sinx)/(cosx) =coty-tanx \\ \\ But: \\ \\ (cosy)/(siny)=coty \\ \\ (sinx)/(cosx)=tanx \\ \\ Hence: \\ \\ \boxed{coty-tanx=coty-tanx} \ Proved!`

PART d)

We have the following expression:

`\ln\left|1+cos \theta\right|+\ln\left|1-cos \theta\right|=2\ln\left|sin \theta\right|`

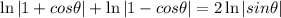
By Logarithm product rule, we know:

`log_(b)(x.y) = log_(b)(x) + log_(b)(y)`

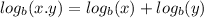
So:

`\ln\left|1+cos \theta\right|+\ln\left|1-cos \theta\right|=\ln\left|(1+cos \theta)(1-cos \theta)\right|`

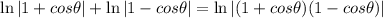
The Difference of Squares states that:

`a^2-b^2=(a+b)(a-b) \\ \\ So: \\ \\ (1+cos \theta)(1-cos \theta)=1-cos^2 \theta`

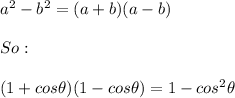
Then:

`\ln\left|(1+cos \theta)(1-cos \theta)\right|=\ln\left|1-cos^(2) \theta\right|`

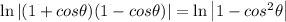
By the Pythagorean identity:

`sin^2(\theta)+cos^2(\theta)=1 \\ \\ So: \\ \\ sin^2 \theta = 1-cos^2 \theta`

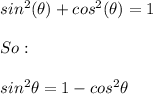
Then:

`\ln\left|1-cos^(2) \theta\right|=\ln\left|sin^2 \theta|`

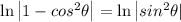
By Logarithm power rule, we know:

`log_(b)(x.y) = ylog_(b)(x)`

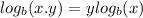
Then:

`\ln\left|sin^2 \theta|=2\ln\left|sin \theta|`

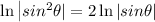
In conclusion:

`\boxedsin \theta\right \ Proved!`