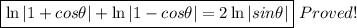Hi! It will be a pleasure to help you to prove these identities, so let's get started:
PART a)
We have the following expression:
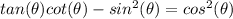
We know that:
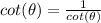
Therefore, by substituting in the original expression:
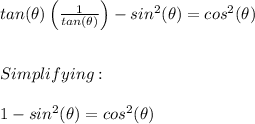
We know that the basic relationship between the sine and the cosine determined by the Pythagorean identity, so:
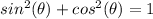
By subtracting
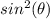 from both sides, we get:
from both sides, we get:
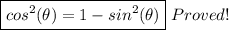
PART b)
We have the following expression:
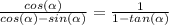
Here, let's multiply each side by
 :
:
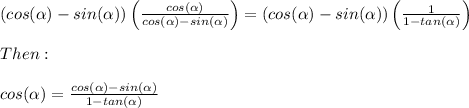
We also know that:
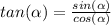
Then:
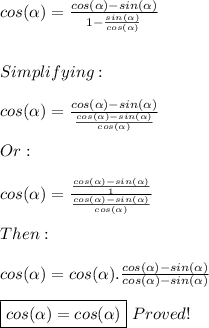
PART c)
We have the following expression:
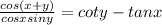
From Angle Sum Property, we know that:
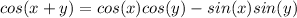
Substituting this in our original expression, we have:
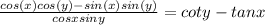
But we can also write this as follows:

PART d)
We have the following expression:
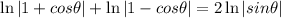
By Logarithm product rule, we know:
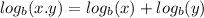
So:
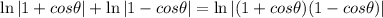
The Difference of Squares states that:
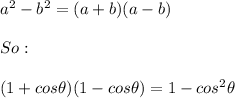
Then:
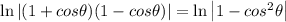
By the Pythagorean identity:
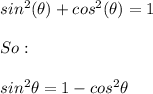
Then:
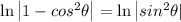
By Logarithm power rule, we know:
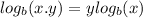
Then:
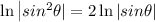
In conclusion: