Question

A mechanical dart thrower throws darts independently each time, with probability 10% of hitting the bullseye in each attempt. The chance that the dart thrower hits the bullseye at least once in 6 attempts is:

Answer 1

The probability of hitting the bullseye at least once in 6 attempts is 0.469.

Explanation:

It is given that a mechanical dart thrower throws darts independently each time, with probability 10% of hitting the bullseye in each attempt.

The probability of hitting bullseye in each attempt, p = 0.10

The probability of not hitting bullseye in each attempt, q = 1-p = 1-0.10 = 0.90

Let x be the event of hitting the bullseye.

We need to find the probability of hitting the bullseye at least once in 6 attempts.

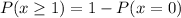`P(x\geq 1)=1-P(x=0)` .... (1)

According to binomial expression

`P(x=r)=^nC_rp^rq^(n-r)`

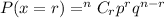
where, n is total attempts, r is number of outcomes, p is probability of success and q is probability of failure.

The probability that the dart thrower not hits the bullseye in 6 attempts is

`P(x=0)=^6C_0(0.10)^0(0.90)^(6-0)`

`P(x=0)=0.531441`

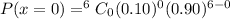
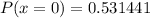
Substitute the value of P(x=0) in (1).

`P(x\geq 1)=1-0.531441`

`P(x\geq 1)=0.468559`

`P(x\geq 1)\approx 0.469`

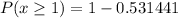
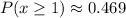
Therefore the probability of hitting the bullseye at least once in 6 attempts is 0.469.