Question

A programmer plans to develop a new software system. In planning for the operating system that he will​ use, he needs to estimate the percentage of computers that use a new operating system. How many computers must be surveyed in order to be 95% confident that his estimate is in error by no more than four percentage points question marks? Assume that nothing is known about the percentage of computers with new operating systems.

Answer 1

n = 601

Explanation:

Since we know nothing about the percentage of computers with new operating system, we assume than 50% of the computers have new operating system.

So, p = 50% = 0.5

q = 1 - p = 1 - 0.5 = 0.5

Margin of error = E = 4 percentage points = 0.04

Confidence Level = 95%

z value associated with this confidence level = z = 1.96

We need to find the minimum sample size i.e. n

The formula for margin of error for the population proportion is:

`E=z\sqrt{(pq)/(n)}`

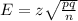
Re-arranging the equation for n, and using the values we get:

`n=((z)/(E) )^(2) * pq\\\\ n=((1.96)/(0.04))^(2) * 0.5 * 0.5\\\\ n = 601`

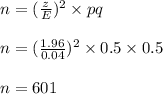
Thus, the minimum number of computers that must be surveyed is 601