Answer:
yes; QR = √200, QS = √8 , RS = √208 ; QR^2 + QS^2 = RS^2
Explanation:
To determine the triangle as a right triangle we have to find the lengths of the sides
The distance formula will be used:
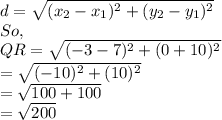
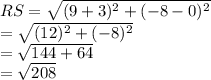
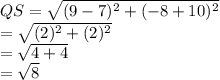
Using Pythagoras theorem, we can see that
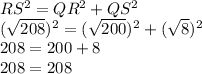
Which proves that given triangle is a right triangle ..