Question

he head librarian at the Library of Congress has asked her assistant for an interval estimate of the mean number of books checked out each day. The assistant provides the following interval estimate: from 740 to 920 books per day. If the head librarian knows the population standard deviation is 150 books checked out per day, how large a sample did her assistant use to determine the interval estimate?

Answer 1

At 95% confidence level, she used 11 people to estimate the confidence interval

Explanation:

The bounds of the confidence interval are: 740 to 920

Mean is calculated as the average of the lower and upper bounds of the confidence interval. So, for the given interval mean would be:

`u=(740+920)/(2)=830`

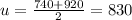
Margin of error is calculated as half of the difference between the upper and lower bounds of the confidence interval. So, for given interval, Margin of Error would be:

`E=(920-740)/(2)=90`

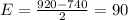
Another formula to calculate margin of error is:

`E=z(\sigma)/(√(n))`

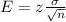
Standard deviation is given to be 150. Value of z depends on the confidence level. Confidence Level is not mentioned in the question, but for the given scenario 95% level would be sufficient enough.

z value for this confidence level = 1.96

Using the values in above formula, we get:

`90=1.96 * (150)/(√(n) )\\\\ n = ((1.96 * 150)/(90))^(2)\\\\ n=11`

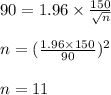
So, at 95% confidence level her assistant used a sample of 11 people to determine the interval estimate