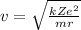Question

An electron with charge −e and mass m moves in a circular orbit of radius r around a nucleus of charge Ze, where Z is the atomic number of the nucleus. Ignore the gravitational force between the electron and the nucleus. Find an expression in terms of these quantities for the speed of the electron in this orbit. (Use any variable or symbol stated above along with the following as necessary: k for Coulomb's constant.)

Answer 1

The speed of an electron in a circular orbit around a nucleus is determined by equating the Coulomb force and the centripetal force, resulting in the expression v = sqrt(kZe^2/mr).

Step-by-step explanation:

The speed v of an electron in a circular orbit around a nucleus can be found by equating the electrostatic force to the centripetal force required for circular motion. The electrostatic force, due to the Coulomb's interaction, between the electron and the nucleus is given by F = k(Ze)(-e)/r^2, where k is Coulomb's constant, Z is the atomic number, e is the magnitude of the charge of an electron, and r is the radius of the orbit. On the other hand, the centripetal force needed to keep the electron in circular motion is F = mv^2/r where m is the mass of the electron and v is its speed.

Setting the two expressions equal gives the equation for the electron's speed v:
k(Ze)(-e)/r^2 = mv^2/r
Solving for v results in the expression:
v = sqrt(kZe^2/mr)

This equation shows that the electron's speed in its orbit depends on the atomic number Z, Coulomb's constant k, the electron's mass m, and the orbit radius r.

Answer 2

`v=\sqrt{(kZe^2)/(mr)}`

Step-by-step explanation:

The electrostatic attraction between the nucleus and the electron is given by:

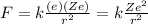`F=k((e)(Ze))/(r^2)=k(Ze^2)/(r^2)` (1)

where

k is the Coulomb's constant

Ze is the charge of the nucleus

e is the charge of the electron

r is the distance between the electron and the nucleus

This electrostatic attraction provides the centripetal force that keeps the electron in circular motion, which is given by:

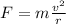`F=m(v^2)/(r)` (2)

where

m is the mass of the electron

v is the speed of the electron

Combining the two equations (1) and (2), we find

`k(Ze^2)/(r^2)=m(v^2)/(r)`

And solving for v, we find an expression for the speed of the electron:

`v=\sqrt{(kZe^2)/(mr)}`