Question

Send it quick guys...

Answer 1

194

Explanation:

Recall 2 rules to solve this easily:

1.
`(a+b)^2=a^2+2ab+b^2`

2.
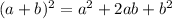
`(a-b)^2=a^2-2ab+b^2`

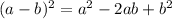
Now, if we let a = 7 and
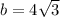`b=4√(3)`, we can say the problem is basically of the form:

`(a+b)^2 + (a-b)^2`

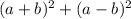
This can be simplified using the rules:

`(a+b)^2 + (a-b)^2\\a^2+2ab+b^2+a^2-2ab+b^2\\2a^2+2b^2`

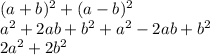
Now we can plug the values of a and b we initially thought of (remember though
`√(x) √(x) =x`):

`2a^2+2b^2\\2(7)^2+2(4√(3))^2\\ 2(49)+2(4√(3))(4√(3))\\98+2(4)(4)(√(3) )(√(3) )\\98+2(4)(4)(3)\\98+96 \\194`

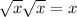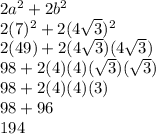
194 is the final answer.