Answer:
A
Explanation:
Given
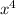 - 1 ← a difference of squares which factors in general as
- 1 ← a difference of squares which factors in general as
a² - b² = (a - b)(a + b)
here
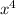 = (x²)² ⇒ a = x² and b = 1
= (x²)² ⇒ a = x² and b = 1
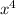 - 1 = (x² - 1)(x² + 1)
- 1 = (x² - 1)(x² + 1)
x² - 1 ← is a difference of squares and factors as
x² - 1 = (x - 1)(x + 1), so
(x² - 1)(x² + 1) = (x - 1)(x + 1)(x² + 1), hence
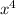 - 1 = (x - 1)(x + 1)(x² + 1) → A
- 1 = (x - 1)(x + 1)(x² + 1) → A