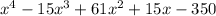Answer:
Answer in factored form:
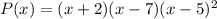
Answer in standard form:

Explanation:
I don't see your choices but I can still give you a polynomial fitting your criteria. I will give the answer in both factored form and standard form.
The following results are by factor theorem:
So if x=-2 is a zero then x+2 is a factor.
If x=7 is a zero then x-7 is a factor.
If x=5 is a zero then x-5 is a factor. It says we have this factor twice. I know this because it says with multiplicity 2.
So let's put this together. The factored form of the polynomial is
A(x+2)(x-7)(x-5)(x-5)
or
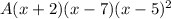
Now A can be any number satisfying a polynomial with zeros -2 and 7 with multiplicity 1, and 5 with multiplicity 5.
However, it does say we are looking for a polynomial function with leading coefficient 1 which means A=1.
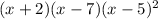
Now the factored form is easy.
The standard form requires more work (multiplying to be exact).
I'm going to multiply (x+2)(x-7) using foil.
First: x(x)=x^2
Outer: x(-7)=-7x
Inner: 2(x)=2x
Last: 2(-7)=-14
--------------------Adding.
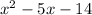
I'm going to multiply
 using formula
using formula
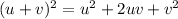 .
.
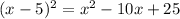 .
.
So now we have to multiply these products.
That is we need to do:
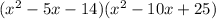
I'm going to distribute every term in the first ( ) to
every term in the second ( ).
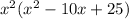
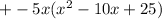
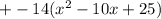
------------------------------------------ Distributing:
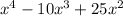
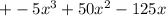
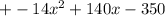
-------------------------------------------Adding like terms: