Question

Using the simple random sample of weights of women from a data​ set, we obtain these sample​ statistics: nequals45 and x overbarequals148.79 lb. Research from other sources suggests that the population of weights of women has a standard deviation given by sigmaequals31.37 lb. a. Find the best point estimate of the mean weight of all women. b. Find a 90​% confidence interval estimate of the mean weight of all women.

Answer 1

Answer: (141.1, 156.48)

Explanation:

Given sample statistics :
`n=45`

`\overline{x}=148.79\text{ lb}`

`\sigma=31.37\text{ lb}`

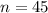
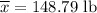
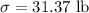
a) We know that the best point estimate of the population mean is the sample mean.

Therefore, the best point estimate of the mean weight of all women =
`\mu=148.79\text{ lb}`

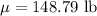
b) The confidence interval for the population mean is given by :-

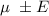`\mu\ \pm E`, where E is the margin of error.

Formula for Margin of error :-

`z_(\alpha/2)*(\sigma)/(√(n))`

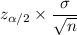
Given : Significance level :
`\alpha=1-0.90=0.1`

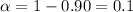
Critical value :
`z_(\alpha/2)=z_(0.05)=\pm1.645`

Margin of error :
`E=1.645*(31.37)/(√(45))\approx 7.69`

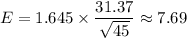
Now, the 90% confidence interval for the population mean will be :-

`148.79\ \pm\ 7.69 =(148.79-7.69\ ,\ 148.79+7.69)=(141.1,\ 156.48)`

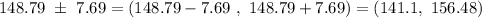
Hence, the 90​% confidence interval estimate of the mean weight of all women= (141.1, 156.48)