Answer: (141.1, 156.48)
Explanation:
Given sample statistics :
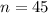
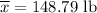
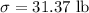
a) We know that the best point estimate of the population mean is the sample mean.
Therefore, the best point estimate of the mean weight of all women =
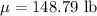
b) The confidence interval for the population mean is given by :-
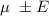 , where E is the margin of error.
, where E is the margin of error.
Formula for Margin of error :-
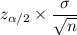
Given : Significance level :
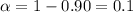
Critical value :
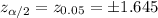
Margin of error :
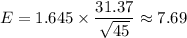
Now, the 90% confidence interval for the population mean will be :-
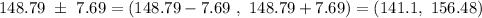
Hence, the 90% confidence interval estimate of the mean weight of all women= (141.1, 156.48)