Question

The weights of 69 randomly selected axles were found to have a variance of 2.46. Construct the 99%confidence interval for the population variance of the weights of all axles in this factory. Round your answers to two decimal places.Answer(How to Enter)2 Points

Answer 1

Answer: (1.64,4.01)

Explanation:

The confidence interval for the population variance is given by :-

`\left ( ((n-1)s^2)/(\chi^2_(n-1,\alpha/2)),\ ((n-1)s^2)/(\chi^2_(n-1,1-\alpha/2)) \ \right )`

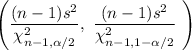
Given : n= 69 ;
`s^2=2.46`

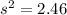
Significance level :
`\alpha=1-0.99=0.01`

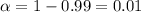
Using Chi-square distribution table ,

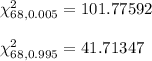`\chi^2_(68,0.005)}=101.77592\\\\\chi^2_(68,0.995)}=41.71347` [by using chi-square distribution table]

Now, the 95% confidence interval for the standard deviation of the height of students at UH is given by :-

`\left ( ((68)(2.46))/(101.77592),\ ((68)(2.46))/(41.71347) \ \right )\\\\=\left ( 1.64361078731, 4.01021540524\right )\approx(1.64,\ 4.01)`

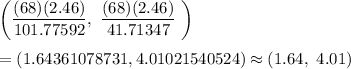
Hence, the 99% confidence interval for the population variance of the weights of all axles in this factory is (1.64,4.01).