Answer: 0.5507
Explanation:
Given : The waiting time, in hours, between successive speeders spotted by a radar unit is a continuous random variable X with a cumulative distribution function

Since , the waiting time is in hours , then we can write 12 minutes as
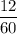 hour i.e.0.2 hour.
hour i.e.0.2 hour.
Now, the probability of waiting fewer than 12 minutes between successive speeders is given by :-
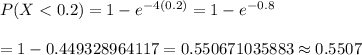
Hence, the required probability = 0.5507