Answer:
Probability is 0.0174
Explanation:
Given data
mean = 140
variance = 25
no of sample n = 49
to find out
probability of the sample
solution
standard deviation is
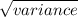
standard deviation =
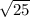
standard deviation = 5
we mean by more than 1.7 millimeters so
mean (X1) = mean + 1.7 or mean - 1.7
so probability = X1 -mean/ ( standard deviation /
 )
)
probability = 140 -1.7 -140 / ( 5 /
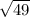 )
)
probability = - 1.7 / 35 = -0.048
probability = 140 + 1.6 -140 / ( 5 /
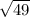 )
)
probability = 1.7 /35 = 0.048
so required probability is i.e
= P(X1 < mean - 1.7 ∪ X1 > mean + 1.7 )
= 1 - P(mean -1.7 < X1 < mean +1.7 )
= 1 - P(-0.048 < X1 < 0.048 )
= 1 - 0.9826
= 0.0174
so required probability is 0.0174