Answer:
33.429 N-m
Step-by-step explanation:
Given :
Inclination angle of two shaft, α = 20°
Speed of shaft A,
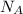 = 1000 rpm
= 1000 rpm
Mass of flywheel, m = 30 kg
Radius of Gyration, k =100 mm
= 0.1 m
Now we know that for maximum velocity,
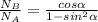
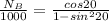
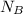 = 1064.1 rpm
= 1064.1 rpm
Now we know
Mass of flywheel, m = 30 kg
Radius of Gyration, k =100 mm
= 0.1 m
Therefore moment of inertia of flywheel, I = m.
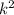
=30 X
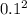
= 0.3 kg-

Now torque on the output shaft
T₂ = I x ω
= 0.3 X 1064.2 rpm
=
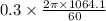
= 33.429 N-m
Torque on the Shaft B is 33.429 N-m