Question

Suppose 23.8 g of oxygen (O2) is heated at constant atmospheric pressure from 27.4°C to 149°C. (a) How many moles of oxygen are present? (Take the molar mass of oxygen to be 32.0 g/mol) (b) How much energy is transferred to the oxygen as heat? (The molecules rotate but do not oscillate.) (c) What fraction of the heat is used to raise the internal energy of the oxygen?

Answer 1

For a: The number of moles of oxygen gas is 0.74375 moles.

For b: The energy transferred to oxygen as heat is
`2.631* 10^3`

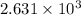
For c: The fraction of heat used to raise the internal energy of oxygen is 0.714.

Step-by-step explanation:

• For a:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

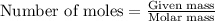
Given mass of oxygen gas = 23.8 g

Molar mass of oxygen gas = 32 g/mol

Putting values in above equation, we get:

`\text{Moles of oxygen gas}=(23.8g)/(32g/mol)=0.74375mol`

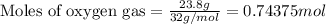
Hence, the number of moles of oxygen gas is 0.74375 moles.

• For b:

Oxygen is a diatomic gas.

To calculate the amount of heat transferred, we use the equation:

`Q=nC_p\Delta T`

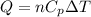
where,

Q = heat absorbed or released

n = number of moles of oxygen gas = 0.74375 moles

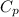`C_p` = specific heat capacity at constant pressure =
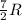`(7)/(2)R` (For diatomic gas)

R = gas constant = 8.314 J/mol K

`\Delta T` = change in temperature =
`(149-27.4)^oC=121.6^oC=121.6K`

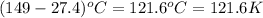
Putting values in above equation, we get:

`Q=0.74375mol* ((7)/(2))* 8.314J/mol.K* 121.6K\\\\Q=2631.71J=2.631* 10^3J`

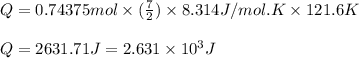
Hence, the energy transferred to oxygen as heat is
`2.631* 10^3`

• For c:

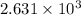
To calculate the fraction of heat, we use the equation:

`f=(U)/(Q)`

where,

U = internal energy =
`nC_v\Delta T`

Calculating the value of U:

n = number of moles of oxygen gas = 0.74375 moles

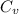`C_v` = specific heat capacity at constant pressure =
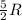`(5)/(2)R` (For diatomic gas)

R = gas constant = 8.314 J/mol K

`\Delta T` = change in temperature =
`(149-27.4)^oC=121.6^oC=121.6K`

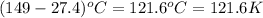
Putting values in above equation, we get:

`U=0.74375mol* ((5)/(2))* 8.314J/mol.K* 121.6K\\\\U=1879.79J=1.879* 10^3J`

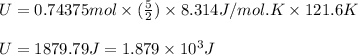
Taking the ratio of 'U' and 'Q', we get:

`f=(1.879* 10^3)/(2.631* 10^3)\\\\f=0.714`

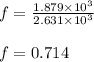
Hence, the fraction of heat used to raise the internal energy of oxygen is 0.714.