Question

Solve the differential equation by variation of parameters.

y''+y=secx

Answer 1

Answer:y=

Acosx+Bsinx +cosx ln(cosx)+x sinx

Explanation:

given equation y''+y=secx

auxiliary equation

`p^2+1=0\\p=\pm i`

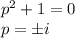
so CF is y=Acosx+Bsinx

now

`y_1(x)=cosx \ \ \ \ y_2(x)=sinx\\{y_1}'(x)=-sinx \ \ \ \ {y_2}'(x)=cosx`

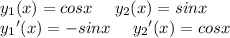
using wronskian formula

`W=\begin{vmatrix}cosx &sinx \\ -sinx & cosx\end{vmatrix}`

=
`cos^2x+sin^2x=1`

now f(x)=secx

`u=-\int (f(x)y_2(x))/(W(x))dx \ and \ v=\int (f(x)y_1(x))/(W(x))dx`

`u=-\int (secx* sinx)/(1)dx \ and \ v=\int (secx* cosx)/(1)dx`

`u=-\int tanx dx \ and \ v=\int {1}dx`

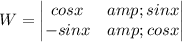
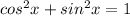
`u=ln(cosx) \ \ \ and \ \ v=x`

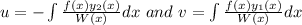
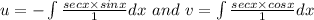
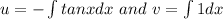
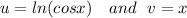
now particular integrals are

PI=cosx ln(cosx)+x sinx

total solution

y= C.F+P.I

y=Acosx+Bsinx +cosx ln(cosx)+x sinx