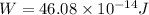Question

How much work is required to bring three protons, initially infinitely far apart, to a configuration where each proton is 1.5×10−15m from the other two? (This is a typical separation for protons in a nucleus.) Express your answer using two significant figures.

Answer 1

`W=46.08* 10^(-14)J`

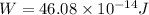
Step-by-step explanation:

The work done(W) in bringing 2 protons to a separation 'r' is given as:

`W=(kq^2)/(r)`

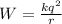
where,

k= coulomb's constant = 9 × 10⁹ N

q = charge of protons = 1.6 × 10⁻¹⁹ C

Now, the third charge (or proton) is brought near the other two protons

Thus, work done against both these is

`W_2+W_3=(kq^2)/(r)+(kq^2)/(r)`

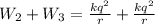
Now,

The total work done (W) =
`W_1 +W_2+W_3=3(kq^2)/(r)`

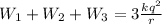
or

`W=3* \frac{9* 10^9* (1.6* 10^(-19))^2}{1.5* 10{-15}}`

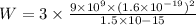
or

`W=46.08* 10^(-14)J`