Answer:
general solution=
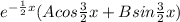 +5
+5
Explanation:
using linear differential equation method
y'' + y' + y = 5
writing down the characteristics equation.
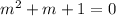
using quadratic formula
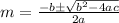
we get
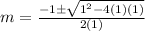
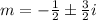
now Complementary function(CF)
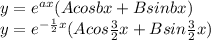
now for particular integrals
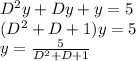
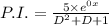
putting D=0
we get
P.I.=5
general solution=CF+PI
general solution=
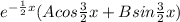 +5
+5