Answer:
Explanation:
Given equations are
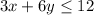
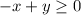
Now the inequalities intersect at x=
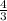
y=
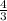
and we have to satisfy this also
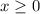
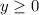
Above all conditions is shown in graph
and the shaded area is the required area
For
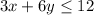 put (0,0)
put (0,0)
it satisfy the point i.e. (0,0) lie on that side which satisfy the inequality similarly check for
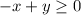
put (4,0) it do not satisfy the inequality therefore it lies on the side which do not satisfy the inequality