Question

Carbonyl fluoride, COF2, is an important intermediate used in the production of fluorine-containing compounds. For instance, it is used to make the refrigerant carbon tetrafluoride, CF4 via the reaction 2COF2(g)⇌CO2(g)+CF4(g), Kc=4.90 If only COF2 is present initially at a concentration of 2.00 M, what concentration of COF2 remains at equilibrium?

Answer 1

Answer : The concentration of
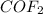`COF_2` remains at equilibrium will be, 0.37 M

Explanation : Given,

Equilibrium constant = 4.90

Initial concentration of
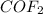`COF_2` = 2.00 M

The balanced equilibrium reaction is,

`2COF_2(g)\rightleftharpoons CO_2(g)+CF_4(g)`

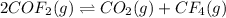
Initial conc. 2 M 0 0

At eqm. (2-2x) M x M x M

The expression of equilibrium constant for the reaction will be:

`K_c=([CO_2][CF_4])/([COF_2]^2)`

Now put all the values in this expression, we get :

`4.90=((x)* (x))/((2-2x)^2)`

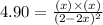
By solving the term 'x' by quadratic equation, we get two value of 'x'.

`x=1.291M\text{ and }0.815M`

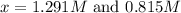
Now put the values of 'x' in concentration of
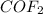`COF_2` remains at equilibrium.

Concentration of
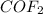`COF_2` remains at equilibrium =
`(2-2x)M=[2-2(1.219)]M=-0.582M`

Concentration of
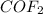`COF_2` remains at equilibrium =
`(2-2x)M=[2-2(0.815)]M=0.37M`

From this we conclude that, the amount of substance can not be negative at equilibrium. So, the value of 'x' which is equal to 1.291 M is not considered.

Therefore, the concentration of
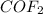`COF_2` remains at equilibrium will be, 0.37 M