Question

Consider the fully Consider the fully developed flow of glycerin at 40°C through a 78-m-long, 4-cm-diameter, horizontal, circular pipe. If the flow velocity at the centerline is measured to be 6 m/s, determine the pressure difference across this 78-m-long section of the pipe and the useful pumping power required to maintain this flow. The density and dynamic viscosity of glycerin at 40°C are ? rho =1252 kg/m3 and mu = 0.3073 kg/ms, respectively. The pressure difference is _____kPa. The required useful pumping power is______ kW

Answer 1

Answer: it would be 12 mph because it’s fast.

Explanation: it’s really fast and easy

Answer 2

The pressure difference is 2876.35 KPa.

The required useful pumping power is 21.69 KW

Step-by-step explanation:

The pressure difference is given by Darcy-Weisbach Equation, which is as follows:

First we get major Head Loss:

HL =
`f(l)/(d)(V^(2))/(2g)`

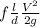
Here,

l = length = 78 m

D = diameter = 4 cm = 0.04 m

V = velocity = 6 m/s

g = acceleration due to gravity = 9.8 m/s²

f = friction coefficient which needs to be determined from moody's chart

For that purpose first we need to find Reynold's Number (Re):

Re = ρVD/μ

Re = (1252 kg/m3)(6m/s)(0.04m)/0.3073kg/ms

Re = 977.8

Since, Re < 2000, it shows that the flow is laminar.

Thus, we refer to the straight line given in moody's chart for laminar flow and find the friction coefficient. For that straight line formula of friction coefficient is

f = 64/Re

f = 64/977.8

f = 0.065

Thus using values in darcy equation:

HL =
`(0.065)(78 m)/(0.04 m)((6m/s)^(2) )/(2(9.8m/s^(2)) )`

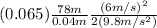
HL = 234.43 m

Now, the pressure difference will be:

ΔP = (HL)ρg = (234.43 m)(1252 kg/m3)(9.8 m/s²)

ΔP = 2876.35 KPa

Now, the useful pumping power is given by:

Power = ΔP(Volume Flow Rate) = ΔP(Area)(Velocity)

Power = ΔP(πD²/4)(V) = (2876350 N/m²){π(0.04 m)²/4}(6 m/s)

Power = 21.69 KW